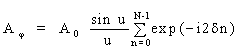 (9)
(9)
Рассмотрим дифракцию Фраунгофера на объекте, представляющем собой совокупность N нескольких бесконечно длинных щелей, имеющих одинаковую ширину b и расположенных на одинаковом расстоянии друг от друга. Такой объект принято называть дифракционной решеткой. Обозначим через d расстояние между центрами соседних щелей (т.н. период решетки). Пусть на дифракционную решетку падает нормально монохроматическое излучение с длиной волны l. Для определения интенсивности света, распространяющегося в направлении, составляющем угол j с нормалью, воспользуемся принципом Гюйгенса-Френеля.
Амплитуды волн, приходящих в т. Nj от каждой из щелей, равны и выражаются формулой (4'), однако разность фаз между волнами, приходящими от соседних щелей, будет равна кdsinj.
Введем обозначение d = 1/2 кdsinj = pdsinj/l.
Чтобы получить возмущение, посылаемое всей решеткой, необходимо просуммировать по всем N щелям, т.е.
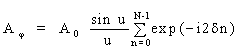 (9) (9)
|
Cумма в (9) представляет собой геометрическую прогрессию, первый член которой равен единице, а показатель прогрессии - q=exp (-i2d). Таким образом
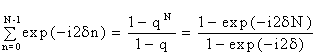 (10) (10)
|
В итоге для возмущения в направлении j получаем
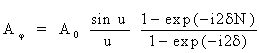 (11) (11)
|
С учетом того, что
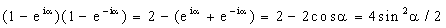
|
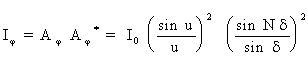 (12) (12)
|
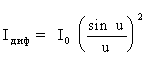 (13) (13)
|
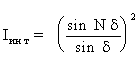 (14) (14)
|
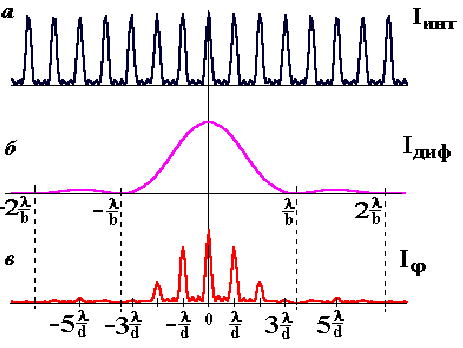
Исследуем более подробно вид функции (14), изображенный на рис.6а. Числитель в формуле (14) обращается в нуль при d=0, p/N, 2p/N, ...., (N-1)p/N, p, (N+1)p/N,... однако для каждого N-ого значения d=0, p, 2p,... в нуль обращается и знаменатель. Воспользовавшись предельным переходом, можно получить, что для этих значений угла функция (14) имеет одинаковое максимальное значение, равное N2. Таким образом, для этих значений угла d интенсивность будет максимальной. Между этими максимумами, называемыми главными, располагаются (N-1) добавочных минимумов, соответствующих нулевым значениям числителя в формуле (14). Так как между любыми двумя соседними добавочными минимумами имеется добавочный максимум, интенсивность которого существенно меньше интенсивности ближайших главных максимумов, то общее число добавочных максимумов между главными равно (N-2).
|
| Рис.6. Дифракция Фраунгофера на четырех щелях: а - интерференционный член (14), б - дифракционный член (13), в -общий вид дифракционной картины (12). |
Вид функции (12), описывающей распределение интенсивности при дифракции Фраунгофера на N щелях, изображен на рис.6в. Характерными точками этого графика являются:
| главные дифракционные минимумы | sinj =l/b, 2l/b, 3l/b, .... |
| добавочные интерференционные минимумы | sinj = l/Nd, 2l/Nd, 3l/Nd, ...., (N-1)l/Nd, (N+1)l/Nd,..., (2N-1)l/Nd, (2N+1)l/Nd,... |
| главные интерференционные максимумы | sinj= 0, l/d, 2l/d, 3l/d, .... |
Таким образом, получив на экране дифракционную картину от решетки и подсчитав число добавочных минимумов или максимумов между главными максимумами, можно определить число щелей решетки.

