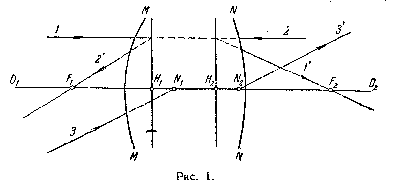
1. Передний и задний фокусы системы F₁ и F₂ (рис. 1). Если на систему падает пучок лучей, параллельных оптической оси системы (лучи 1), то они соберутся в заднем фокусе системы F₂, если параллельный пучок идет в обратном направлении (лучи 2), то лучи соберутся в переднем фокусе системы F₁. Плоскости, проходящие через фокусы перпендикулярно оптической оси системы, называются фокальными плоскостями.

2. Главные точки системы H₁ и H₂ и главные плоскости (т. е. плоскости, проходящие через главные точки перпендикулярно оптической оси). Главные плоскости изображают друг друга с линейным увеличением, равным +1. Найти главные плоскости можно следующим образом. Рассмотрим луч 1, падающий на оптическую систему MMNN параллельно оптической оси О₁О₂. После преломления его направление распространения будет 1'. Точка пересечения лучей 1 и 1' лежит во второй главной плоскости. Рассмотрев луч 2, идущий в обратном направлении, можно получить положение первой главной плоскости. Расстояния F₁H₁ = f₁, и F₂H₂ = f₂ от главных точек до фокусов называются фокусными расстояниями системы. Если данная оптическая система находится в среде с постоянным показателем преломления, то |f₂| == |f₁|.

3. Узловые точки системы. N₁ и N₂. Если какой-либо луч (или его продолжение) (рис. 1) проходит через первый узел N₁ (луч 3), то после преломления в оптической системе этот луч (или его продолжение) будет выходить из второго узла N₂ в направлении, параллельном направлению падающего луча (луч 3'). Положение узлов относительно фокусов определяется соотношениями F₁N₁ = f₂; F₂N₂ = f₁.

Если система расположена в среде с постоянным показателем преломления, то узловые точки совпадают с главными.

Доказательство существования этих кардинальных точек, а также их свойства приведены в литературе, указанной в конце описания. В тонких линзах положение обеих главных точек и обеих узловых точек совпадает с центром линзы.