![]()
Рассмотрение вероятностных проблем в случае непрерывной переменной и легко свести к более простому случаю, когда переменная принимает дискретные значения и является, таким образом, счетной. Для этого всю область изменения переменной и следует разбить на бесконечно малые и равные интервалы величиной δи (бины). Каждый такой интервал обозначается соответствующим индексом i. Значение и в этом интервале обозначим через иi, а вероятность того, что и лежит в этом интервале, через Рi или Р(иi). Такая операция дает нам возможность иметь дело со счетным числом значений переменной ui; каждое такое значение отвечает одному из интервалов i =1, 2, 3, ...
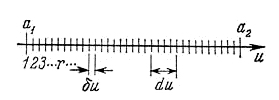
Рис.4. Разбиение непрерывной переменной на дискретные интервалы δи (бины). Макроскопически малый интервал du включает достаточно много бинов, но является настолько малым, что изменением функции Р(иi) на этом интервале можно пренебречь.
Вероятность dP того, что переменная и находится в интервале значений между u и и + du будет равна сумме вероятностей Р(иi) для всех иi которые входят в этот интервал. Если du достаточно мало, то изменением функции Р(иi) на этом интервале можно пренебречь и считать, что все Р(иi) равны и имеют значение, которое мы обозначим Р. Тогда искомая вероятность dP = Рm, где m=du/δи – число бинов, входящих в рассматриваемый интервал. Т.к. dP пропорциональна величине du, то ее можно записать в виде dP = f(u)du, где f(u) называется плотностью вероятности и не зависит от величины интервала du. Следует отметить, что вероятность того, что переменная и находится в интервале значений между u и и + du равна площади под кривой f(u) ограниченной интервалом du: dP = f(u)du. Это справедливо и для конечного интервала - вероятность того, что переменная и находится в интервале значений от a до b равна площади под кривой f(u) ограниченной этим интервалом:
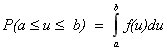 .
.
Формулы, полученные выше для дискретных переменных, остаются в силе и для переменных, принимающих непрерывные значения, если суммы, которые входят в эти формулы, заменить на интегралы:
|
|
Дискретная случайная величина n принимает значения n1 , n2 ,...nα . |
Непрерывная случайная величина u принимает значения от -∞ до +∞. |
|
Вероятность |
|
dP = f(u)du |
|
Условие нормировки |
|
|
|
Среднее значение |
|
|
|
Дисперсия |
|
|
|
Среднеквадратичное отклонение (стандартное) |
|
|
|
Среднее значение функции Ф от случайной переменной |
|
|