Рассмотрим в качестве примера
дискретной случайной величины,
количество очков n, которое выпадает при бросании игральной кости. Ниже
представлен результат бросания десяти игральных костей (или
N=10 бросаний одной кости). Результаты опыта удобно представить в виде
графика - гистограммы. Для построения гистограммы область значений
случайной величины (ось X) разбивают на одинаковые интервалы (бины),
а по оси Y откладывают
Ni
- количество попаданий случайной
величины в i-ый интервал.
Представленная на рисунке комбинация кубиков является выборкой - одной из
многих возможных реализаций опыта. Вычислим по данной выборке среднее количество
очков выпадающее на одном кубике (выборочное среднее)
n
и среднеквадратичное отклонение от среднего (выборочное
стандартное отклонение):
 |
 |
|
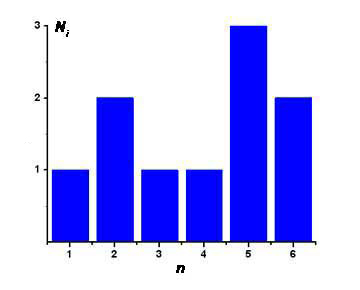
Рис.1. Результаты опыта в виде гистограммы |
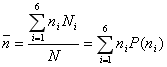
где |
Учитывая, что P(1)=1/10, P(2)=2/10, P(3)=1/10, P(4)=1/10, P(5)=3/10, P(6)=2/10, получаем: n = 3.9, σ = 1.7. Величина P(ni) показывает долю случаев выпадения ni и при N→ ∞ стремится к P(ni) - вероятности получить ni. Таким образом при N→ ∞ выборочные значения стремятся к своим предельным значениям, которые и будут соответственно вероятностью, средним значением и стандартным отклонением.
Пример: для идеального кубика все грани равновероятны, поэтому для любой грани вероятность равна 1/6. Именно к этому значению будет стремиться P(ni) при N→ ∞.
|
Рис.2. Нормированная гистограмма |
Рис.3. Распределение вероятности P(n) |
На рис.2 показана нормированная гистограмма, у которой по оси Y отложены значения P(ni). При N→ ∞ эта гистограмма показывает распределение вероятности, которое характеризуется функцией P(n) (рис.3), определяющей вероятность появления значения n дискретной случайной величины. С помощью этой функции можно найти вероятность появления значения n в некотором интервале, например от a до b. Эта вероятность равна сумме вероятностей P(n) для всех значений n, лежащих в заданном интервале
Если интервал включает все возможные значения n, то эта вероятность равна единице, так как в результате опыта обязательно появится одно из возможных значений n. Таким образом сумма P(n) по всем значениям n равна единице
Это соотношение называется условием нормировки.
Стандартное отклонение среднего
Как уже отмечалось выше, n и σ характеризуют предельное распределение, которое получается при бесконечном числе измерений N. На практике имеется конечное число измеренных значений n1 , n2 ,…nN т.е.выборка {ni}(i= 1, 2,... N ). Можно показать, что для данной выборки наилучшей оценкой для n и σ будут их выборочные значения, которые можно записать следующим образом:
Выборочное стандартное отклонение характеризует разброс измеренных значений относительно среднего и при N→ ∞ стремится к своему предельному значению σ.
Очевидно, что для другой выборки мы получим другое среднее. Получив несколько выборок, мы могли бы найти среднее для каждой выборки и получить таким образом выборку для средних. По этой выборке можно найти среднее ("среднее для средних значений") и стандартное отклонение σn (стандартное отклонение среднего) , которое будет характеризовать разброс средних значений относительно среднего всех средних или истинного значения.
Так как n есть функция измеренных значений ni, то для данной выборки{ni} мы можем оценить стандартное отклонение среднего с помощью формулы для расчета ошибок при косвенных измерениях:
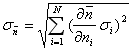
Так как ni представляют собой результаты измерения одной и той же величины n, то σi = σ, откуда:
Следует отметить, что в отличии от σ, стандартное отклонение среднего убывает с ростом числа измерений: σn → 0 при N → ∞.
