Цель работы
В эксперименте используется связь между периодом
колебаний крутильного маятника и его моментом инерции.
В качестве маятника выбрана круглая платформа, подвешенная
в поле тяжести на трех длинных нитях (трифилярный подвес).
Платформа может совершать крутильные колебания вокруг
вертикальной оси. На платформу помещаются тела различной формы,
измеряются периоды колебаний маятника и определяются значения моментов
инерции этих тел. Теорема Гюйгенса-Штейнера проверяется
по соответствию между экспериментальной и теоретической
зависимостями моментов инерции грузов от их расстояния до
центра платформы.
Теорема Гюйгенса-Штейнера.
Если момент инерции тела относительно некоторой оси вращения,
проходящей через центр масс, имеет значение
J0, то относительно любой другой оси,
находящейся на расстоянии a от первой и параллельной ей,
он будет равен
 , (2.1)
, (2.1)где m -масса тела.
Для проверки теоремы Гюйгенса-Штейнера в данной работе исследуются
крутильные колебания твердого тела на трифилярном подвесе.
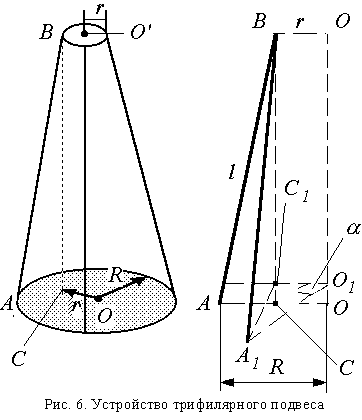 Трифилярный подвес представляет собой круглую платформу радиуса R,
подвешенную на трех симметрично расположенных нитях
одинаковой длины, укрепленных у ее краев (рис.6). Наверху
эти нити также
симметрично прикреплены к диску несколько меньшего размера
(радиуса r).
Платформа может совершать крутильные колебания вокруг
вертикальной оси OO`
, перпендикулярной к ее плоскости и проходящей через ее центр.
Такое движение платформы приводит к изменению положения ее
центра тяжести по высоте.
Трифилярный подвес представляет собой круглую платформу радиуса R,
подвешенную на трех симметрично расположенных нитях
одинаковой длины, укрепленных у ее краев (рис.6). Наверху
эти нити также
симметрично прикреплены к диску несколько меньшего размера
(радиуса r).
Платформа может совершать крутильные колебания вокруг
вертикальной оси OO`
, перпендикулярной к ее плоскости и проходящей через ее центр.
Такое движение платформы приводит к изменению положения ее
центра тяжести по высоте.
Если платформа массы m, вращаясь в одном направлении,
поднялась на высоту h
, то приращение потенциальной энергии будет равно
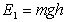 , (2.2)
, (2.2)
где g - ускорение силы тяжести.
Вращаясь в другом направлении, платформа придет в положение
равновесия (h=0)
с кинетической энергией, равной
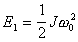 , (2.3)
, (2.3)где J - момент инерции платформы, w0
- угловая скорость вращения платформы в момент прохождения
ею положения равновесия.
Пренебрегая работой сил трения, на основании закона
сохранения механической энергии имеем:
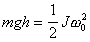 , (2.4)
, (2.4)
Считая, что платформа совершает гармонические крутильные
колебания,
можно записать зависимость углового смещения платформы
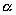 от времени t в виде
от времени t в виде
 , (2.5)
, (2.5)где 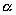 0 - угол максимального поворота
платформы, т.е. амплитуда углового смещения,
T - период колебания. Для угловой скорости w ,
являющаяся первой производной по времени от величины смещения,
можно записать
0 - угол максимального поворота
платформы, т.е. амплитуда углового смещения,
T - период колебания. Для угловой скорости w ,
являющаяся первой производной по времени от величины смещения,
можно записать
 . (2.6)
. (2.6)
В момент прохождения платформы через положение равновесия
(t = 0, 0.5Т,... )
величина w(t) будет максимальна и равна по модулю
 . (2.7)
. (2.7)
Из выражений (2.4) и (2.7) следует, что
 . (2.8)
. (2.8)
Если l - длина нитей подвеса,
R - расстояние от центра платформы до точек крепления
нитей на ней,
r - радиус верхнего диска (рис.6), то легко видеть, что
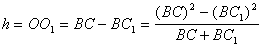 . (2.9)
. (2.9)
Так как
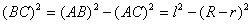 , (2.10)
, (2.10)а при максимальном отклонении платформы от положения равновесия
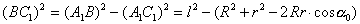 , (2.11)
, (2.11)
то
 . (2.12)
. (2.12)
При малых углах отклонения
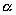 0 значение синуса этого угла можно
заменить просто значением
0 значение синуса этого угла можно
заменить просто значением 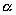 0.
Учитывая также, что при R << l величину знаменателя можно
положить равной 2l,
получаем
0.
Учитывая также, что при R << l величину знаменателя можно
положить равной 2l,
получаем
 . (2.13)
. (2.13)
При этом закон сохранения энергии (2.8) примет вид:
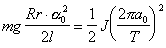 , (2.14)
, (2.14)откуда следует, что
 . (2.15)
. (2.15)По формуле (2.15) можно экспериментально определить момент инерции пустой платформы или платформы с телом, положенным на нее, так как все величины в правой части формулы непосредственно измеряются. Следует помнить, что m - это суммарная масса платформы и исследуемого тела, положенного на нее.
Соотношение (2.15) используется в лабораторной работе для определения
моментов инерции тел простой формы и подтверждения
справедливости теоремы Гюйгенса-Штейнера.
Вид установки показан на рис.6.
или AVI (3.8M)
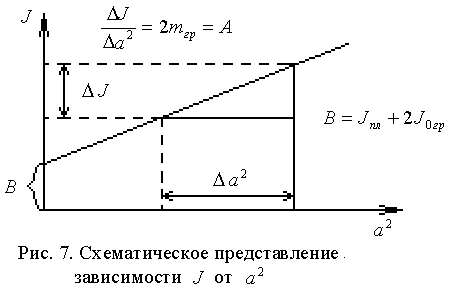
Отношение радиуса платформы к длине нитей подвеса составляет
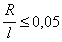 , что соответствует приближениям,
используемым при выводе формулы (2.15).
, что соответствует приближениям,
используемым при выводе формулы (2.15).
Тела на платформу необходимо класть строго симметрично, так, чтобы не было перекоса платформы. Для облегчения определения положения грузов и более точной их установки на платформе нанесены концентрические окружности на определенном расстоянии друг от друга (5 мм).
Вращательный импульс, необходимый для запуска крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг его оси. Это достигается с помощью шнура, связанного с рычагом, закрепленным на верхнем диске. При таком возбуждении колебаний почти полностью отсутствуют другие типы колебаний, наличие которых затрудняет измерения. При измерениях недопустимо пользоваться амплитудами колебаний, большие, чем 100.
Система измерения времени включает в себя электронный таймер с фотодатчиком,
укрепленным на подставке. При проведении измерений датчик устанавливается
в удобное положение. Запуск таймера осуществляется нажатием кнопки "Пуск",
остановка - кнопкой "Стоп". При подготовке к дальнейшим измерениям
результаты предыдущих убираются с табло таймера нажатием кнопки "Сброс".
Упражнение 1. Проверка теоремы Гюйгенса-Штейнера
Измерения
Для проверки теоремы Гюйгенса-Штейнера используют два одинаковых тела (в данной работе они имеют цилиндрическую форму). Перед каждым измерением следует остановить платформу.
Произвести взвешивание грузов.
Установить грузы в центре платформы, положив их один на другой. Создать крутильные колебания платформы. Измерить время tn нескольких колебаний (n=15-20). Данные занести в табл. 2.1.
Таблица 2.1
| Номер опыта | a | a2 | n | tn | Ti = tn / n | Ji |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| ...... | ||||||
-
Расположить грузы симметрично на платформе. Провести измерения времени колебаний tn для 5-7 положений грузов, постепенно перемещая их к краям платформы. Рекомендуется перемещать грузы каждый раз на 1 см. Занести в табл.2.1 значения расстояний а от центра масс каждого тела до центра платформы, число колебаний n и значения времени этих колебаний tn.
Для каждого положения грузов определить период колебаний грузов Ti.
Занести в таблицу значения a2.
Для каждого положения грузов найти значения момента инерции платформы с грузами Ji по формуле (2.15). Величины l, R, r и масса платформы даются, как постоянные установки.
Полученные значения Ji наносят на график зависимости момента инерции системы тел,
 от квадрата расстояния центра масс каждого груза
до оси вращения J(a2)
(схематично эта зависимость представлена на рис.7).
от квадрата расстояния центра масс каждого груза
до оси вращения J(a2)
(схематично эта зависимость представлена на рис.7).
Как следует из теоремы Гюйгенса-Штейнера, этот график должен быть прямой линией, с угловым коэффициентом численно равным 2mгр, так как используются два тела с одинаковой массой mгр.С помощью метода наименьших квадратов (МНК) построить зависимость J от a2, J=B+A*a2. Определить ошибки значений A и B по формулам МНК. Из зависимости J(a2) определить значение
 Сравнить полученное значение с массами грузов
mгр , найденными при взвешивании.
Совпадение этих величин (с учетом погрешностей вычислений)
также указывает на выполнимость теоремы Гюйгенса-Штейнера.
Сравнить полученное значение с массами грузов
mгр , найденными при взвешивании.
Совпадение этих величин (с учетом погрешностей вычислений)
также указывает на выполнимость теоремы Гюйгенса-Штейнера.
Измерения
Момент инерции пустой платформы Jпл определяют по формуле 2.15. Измерить период колебаний пустой платформы Tпл. Сообщают платформе вращательный импульс и измеряют время tn некоторого числа (n=15-20) полных колебаний, что дает возможность достаточно точно определить величину периода Tпл Такие измерения проводят 3-5 раз. Полученные результаты заносят в табл. 2.2.
Таблица 2.2
| Тело | № эксп | n | tn | T | {T} | ST | J | SJ |
| 1. Пустая платформа | 1 | |||||||
| 2 | ||||||||
| ...... | ||||||||
| 2. Платформа c квадратной пластиной | 1 | |||||||
| 2 | ||||||||
| ...... | ||||||||
| 3. Платформа c треугольной пластиной | 1 | |||||||
| 2 | ||||||||
| ...... | ||||||||
Платформу поочередно нагружают исследуемыми телами таким образом, чтобы их центр масс совпадал с осью вращения платформы (совпадали отверстия в теле и на платформе). Масса этих тел известна или может быть определена с помощью взвешивания. В качестве исследуемых тел выбирают пластины, имеющие форму квадрата и равностороннего треугольника. Измеряют время tn нескольких колебаний всей системы. Для каждого тела проводят измерения 3-5 раз. Результаты измерений заносят в табл. 2.2.
По экспериментальным данным для каждого опыта найти значение величины периода крутильных колебаний
 .
.
Найти средние арифметические значения и среднеквадратичные отклонения для периодов колебаний пустой платформы ( Tпл ) и платформы с исследуемыми телами ( T2 и T3 ).
-
По формуле (2.15) определить величины Tпл , T2 , T3 и вычислить среднеквадратичные отклонения этих величин.
Вычислить моменты инерции квадратной и треугольной пластин по формулам:
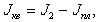 (2.16)
(2.16)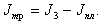 .
.Найти среднеквадратичные отклонения этих величин.
Провести сравнение экспериментально полученных значений Jкв и Jтр и с рассчитанными теоретически (см. Приложение) по формулам:
 (2.17)
(2.17)для квадрата и
 (2.18)
(2.18)для равностороннего треугольника, где m - масса пластины, d - ее сторона.
Провести сопоставления величины Jпл с величиной В, полученной в упр.1, таким образом проверить соотношение
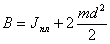 (
( 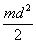 - момент инерции дисков,
используемых при выполнении упр.1).
- момент инерции дисков,
используемых при выполнении упр.1).
В результате выполнения работы должна быть проведена проверка выполнения теоремы Гюйгенса-Штейнера. Должно быть также проведено сравнение экспериментально найденного значения момента инерции для тела заданной формы с соответствующим значением, рассчитанным теоретически.
Контрольные вопросы
Что такое главные оси инерции? Центральные оси? Привести примеры.
-
Что такое момент инерции тела относительно закрепленной оси?
Чему равны моменты инерции следующих тел: тонкая палочка, тонкий диск, тонкие прямоугольная и треугольная пластины, цилиндр, шар, параллелепипед? Как их получить?
Сформулируйте теорему Гюйгенса-Штейнера.
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, § 31,32,34.
Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд.: Наука.1989, § 30,35.